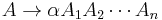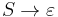Greibach normal form

In computer science and formal language theory, a context-free grammar is in Greibach normal form if the right-hand sides of all productions start with a terminal symbol, optionally followed by some variables. A non-strict form allows one exception to this format restriction for allowing the empty word (epsilon, ε) to be a member of the described language. The normal form bears the name of Sheila Greibach.

More precisely, a context-free grammar is in Greibach normal form, if all production rules are of the form:

$A \to \alpha A_1 A_2 \cdots A_n$

$S \to \varepsilon$

where A is a nonterminal symbol, α is a terminal symbol, 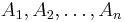$A_1, A_2, \ldots, A_n$ is a (possibly empty) sequence of nonterminal symbols not including the start symbol, S is the start symbol, and ε is the empty word.

Observe that the grammar must be without left recursions.

Every context-free grammar can be transformed into an equivalent grammar in Greibach normal form. (Some definitions do not consider the second form of rule to be permitted, in which case a context-free grammar that can generate the empty word cannot be so transformed.) In particular, there is a construction ensuring that the resulting normal form grammar is of size at most O(n⁴), where n is the size of the original grammar.^[1] This conversion can be used to prove that every context-free language can be accepted by a non-deterministic pushdown automaton.

Given a grammar in GNF and a derivable string in the grammar with length n, any top-down parser will halt at depth n.

Notes

^ Blum and Koch (1999)

References

John E. Hopcroft and Jeffrey D. Ullman, Introduction to Automata Theory, Languages and Computation, Addison-Wesley Publishing, Reading Massachusetts, 1979. ISBN 0-201-02988-X. (See chapter 4.)
Norbert Blum and Robert Koch: Greibach Normal Form Transformation Revisited. Information and Computation 150(1), 1999, pp. 112–118 preprint

Greibach normal form

See also

Notes

References